Membuat Mesin Abstrak Moore dan Mealy
Ihsan
Januari 09, 2020
0
A. Mesin Moore
Mesin moore adalah finite-state machine yang nilai outputnya
ditentukan berdasarkan statenya.
Mesin Moore dinamai Edward F. Moore, yang mempresentasikan
konsep itu dalam sebuah makalah tahun 1956, "Gedanken-experiments on
Sequential Machines"
Diagram Mesin Moore atau Diagram Moore adalah diagram yang
menghubungkan nilai output dengan masing-masing state.
=> Mesin moore ditetapkan ke dalam 6 tuple yang terdiri dari:
- Q=himpunan state
- ∑= himpunan symbol input
- δ=fungsi transisi
- ∑= himpunan symbol input
- δ=fungsi transisi
- S=state awal
- Δ=himpunan output
- λ =fungsi output untuk setiap state
- λ =fungsi output untuk setiap state
=> Cara membuat mesin moore di Jflap
1. Buka aplikasi jflap, lalu pilih Moore Machine
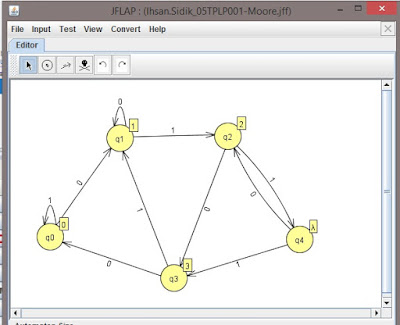
2. Buat mesin moore seperti gambaR dibawah ini
=> 6 tupel dari mesin moore diatas, yaitu :
- Q={q0,q1,q2,q3,q4}
- ∑={0,1}
- S=q0
- ∑={0,1}
- S=q0
- Δ={0,1,2,3,4}
- λ (q0)=0,(q1)=1,(q2)=2,(q3)=3,(q4)=4
- λ (q0)=0,(q1)=1,(q2)=2,(q3)=3,(q4)=4
- δ=Fungsi Transisi
=> Uji input
10100
20 mod 5=0 , jadi berahir di state q0
10101
21mod5=1, jadi berahir di state q1
10110
22 mod5=2, jadi berahir di state q2
10111
23 mod5=3, jadi berahir di state q3
B. Mesin Mealy
Mesin Mealy
adalah otomasi fasa berhingga (finite state automaton atau finite state
tranducer) yang menghasilkan keluaran berdasarkan fasa saat itu dan bagian
masukan/input. output pada Mesin
Mealy akan
berasosiasi dengan transisi. Mesin Mealy sendiri didefinisikan dalam 6
tupel, M = (Q, ∑, δ, S, Δ, λ), dimana:
Q = himpunan
state
∑ = himpunan symbol input
δ = fungsi transisi
S = state awal, S Q
Δ = himpunan output
λ = fungsi output untuk setiap transisi
=> Cara membuat mesin mealy di Jflap
1. Buka aplikasi jflap, lalu pilih Mealy Machine
2. Buat mesin moore seperti gambaR dibawah ini
=> 6
tupel dari mesin mealy diatas, yaitu :
Q =
{q0,q1,q2,q3,q4}
∑ = {0,1}
Δ = {Y,T}
S = q0
λ = Fungsi
output untuk setiap output
λ = (q0,0) = T
λ = (q0,1) = T
λ = (q1,0) = Y
λ = (q1,1) = Y
λ = (q2,0) = T
λ = (q2,1) = Y
λ = (q3,0) = Y
λ = (q3,1) = T
λ = (q4,0) = T
λ = (q4,1) = Y
δ = fungsi transisi
=> Uji input
Lampiran lembar jawaban UAS :
>>>>> Terima Kasih <<<<<












Tidak ada komentar